基础原理讲述FFT快速傅里叶变换FFT算法是DFT算法的改良版如何利用FFT算法实现快速信号分析，而DFT是FFT的离散化理解FFT如何利用FFT算法实现快速信号分析，就从傅里叶变换到DFT再到FFT的思路进行推导笔者也会按照这样的思路进行讲解推导傅里叶变换傅里叶变换是傅里叶级数的推广如何利用FFT算法实现快速信号分析，所以在谈傅里叶变换之间如何利用FFT算法实现快速信号分析，先说一下傅里叶级数在大学期间学习无穷级数。

Y的前一半与后一半是复数共轭关系FFT快速傅里叶变换是利用复数形式的离散傅里叶变换来计算实数形式的离散傅里叶变换，matlab中的fft函数是实现该算法的实现这种算法可以减少计算DFT的时间，大大提高如何利用FFT算法实现快速信号分析了运算效率，并曾经一度被认为是信号分析技术划时代的进步。

所以只要时间序列足够长，采样足够密，频域采样也就可较好地反映信号的频谱趋势，所以FFT可以用以进行连续信号的频谱分析当然，这里作了几次近似处理1用离散采样信号的傅立叶变换来代替连续信号的频谱，只有在严格满足采样定理的前提下，频谱才不会有畸变，否则只是近似2用有限长序列来代替无限长。

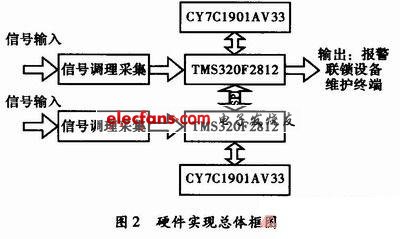
在数字信号分析的世界里，FFT快速傅立叶变换是探索信号频率成分的关键工具然而，它并非直接揭示信号的完整面貌，而是需要通过巧妙地利用窗函数来校准窗函数就像一面滤镜，它们在频谱分析中扮演着至关重要的角色，特别是在处理信号与离散频率点的匹配问题时如果不加控制jinnianhui金年会，这种不匹配可能导致真实信息。

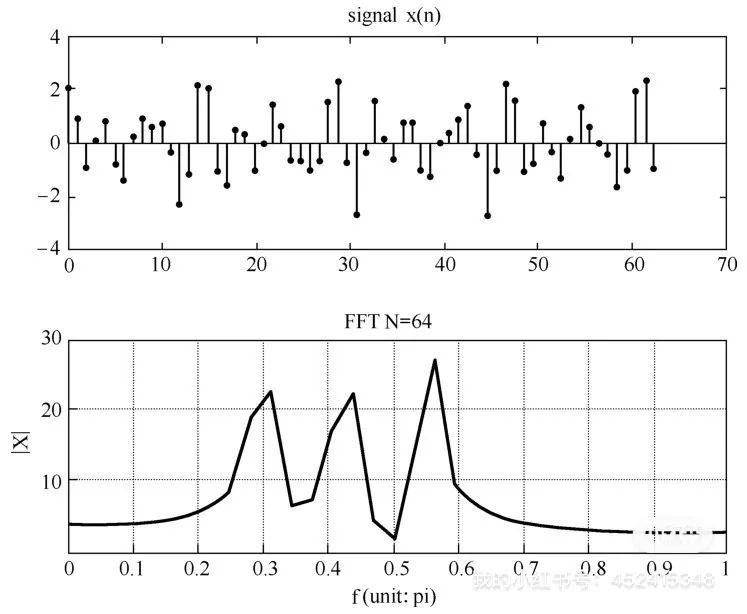
2 对数据进行三维空间划分，将每个空间位置的信号作为一维数据进行分析3 使用快速傅里叶变换FFT算法对每个一维数据进行变换，得到频域数据4 对频域数据进行进一步处理，如阈值设定目标特征提取等，以实现目标检测5 根据检测结果进行后续处理，如目标跟踪识别等需要注意的是，在实际应用。